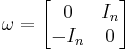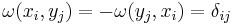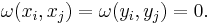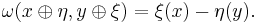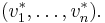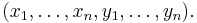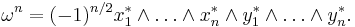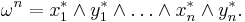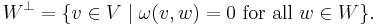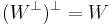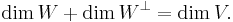Symplectic vector space

In mathematics, a symplectic vector space is a vector space V (over a field, for example the real numbers R) equipped with a bilinear form ω : V × V → R that is

Skew-symmetric: ω(u, v) = −ω(v, u) for all u, v ∈ V.
Totally isotropic ω(v, v) = 0 for all v ∈ V.
Nondegenerate: if ω(u, v) = 0 for all v ∈ V then u = 0.

The bilinear form ω is said to be a symplectic form in this case.

In practice, the above three properties (skew-symmetric, isotropic and nondegenerate) need not all be checked to see that some bilinear form is symplectic:

The skew-symmetric property is redundant (as a condition), as it follows from the isotropic property (applied to v, to w and to v+w and then combined). Hence, the skew-symmetric property needs not be checked if the isotropic property is known to hold.
If the underlying field has characteristic ≠ 2, the isotropic property is actually equivalent to the skew-symmetric property. Thus, the isotropic property needs not be checked if the skew-symmetric property is known to hold and the field has characteristic ≠2. On the other hand, if the characteristic is 2, the skew-symmetric property is implied by, but does not imply, the isotropic property. In this case every symplectic form is a symmetric form, but not vice versa.

Working in a fixed basis, ω can be represented by a matrix. The three conditions above say that this matrix must be skew-symmetric and nonsingular. This is not the same thing as a symplectic matrix, which represents a symplectic transformation of the space.

If V is finite-dimensional then its dimension must necessarily be even since every skew-symmetric matrix of odd size has determinant zero.

A symplectic form behaves quite differently from a symmetric form, such as the dot product on Euclidean vector spaces. With a Euclidean inner product g, we have g(v,v) > 0 for all nonzero vectors v.

1 Standard symplectic space
- 1.1 Analogy with complex structures
2 Volume form
3 Symplectic map
4 Symplectic group
5 Subspaces
6 Heisenberg group
7 See also
8 References

Standard symplectic space

Further information: Symplectic matrix#Symplectic transformations

The standard symplectic space is R²ⁿ with the symplectic form given by a nonsingular, skew-symmetric matrix. Typically ω is chosen to be the block matrix

$\omega = \begin{bmatrix} 0 & I_n \\ -I_n & 0 \end{bmatrix}$

where I_n is the n × n identity matrix. In terms of basis vectors 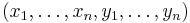$(x_1, \ldots, x_n, y_1, \ldots, y_n)$ :

$\omega(x_i, y_j) = -\omega(y_j, x_i) = \delta_{ij}\,$

$\omega(x_i, x_j) = \omega(y_i, y_j) = 0.\,$

A modified version of the Gram-Schmidt process shows that any finite-dimensional symplectic vector space has a basis such that $\omega$ takes this form, often called a Darboux basis.

There is another way to interpret this standard symplectic form. Since the model space Rⁿ used above carries much canonical structure which might easily lead to misinterpretation, we will use "anonymous" vector spaces instead. Let V be a real vector space of dimension n and V^∗ its dual space. Now consider the direct sum W := V ⊕ V^∗ of these spaces equipped with the following form:

$\omega(x \oplus \eta, y \oplus \xi) = \xi(x) - \eta(y).$

Now choose any basis (v₁, ..., v_n) of V and consider its dual basis

$(v^*_1, \ldots, v^*_n).$

We can interpret the basis vectors as lying in W if we write x_i = (v_i, 0) and y_i = (0, v_i^∗). Taken together, these form a complete basis of W,

$(x_1, \ldots, x_n, y_1, \ldots, y_n).$

The form $\omega$ defined here can be shown to have the same properties as in the beginning of this section; in other words, every symplectic structure is isomorphic to one of the form V ⊕ V^∗. The subspace V is not unique, and a choice of subspace V is called a polarization. The subspaces that give such an isomorphism are called Lagrangian subspaces or simply Lagrangians.

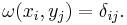
Explicitly, given a Lagrangian subspace (as defined below), then a choice of basis $(x_1, \ldots, x_n)$ defines a dual basis for a complement, by $\omega(x_i,y_j) = \delta_{ij}.$

Analogy with complex structures

Just as every symplectic structure is isomorphic to one of the form V ⊕ V^∗, every complex structure on a vector space is isomorphic to one of the form V ⊕ V. Using these structures, the tangent bundle of an n-manifold, considered as a 2n-manifold, has an almost complex structure, and the cotangent bundle of an n-manifold, considered as a 2n-manifold, has a symplectic structure: 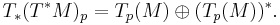$T_*(T^*M)_p = T_p(M) \oplus (T_p(M))^*.$

The complex analog to a Lagrangian subspace is a real subspace, a subspace whose complexification is the whole space: W = V ⊕ J'V.

Volume form

Let ω be a form on a n-dimensional real vector space V, ω ∈ Λ²(V). Then ω is non-degenerate if and only if n is even, and ω^n/2 = ω ∧ ... ∧ ω is a volume form. A volume form on a n-dimensional vector space V is a non-zero multiple of the n-form e₁^∗ ∧ ... ∧ e_n^∗ where e₁, e₂, ..., e_n is a basis of V.

For the standard basis defined in the previous section, we have

$\omega^n=(-1)^{n/2} x^*_1\wedge\ldots \wedge x^*_n \wedge y^*_1\wedge \ldots \wedge y^*_n.$

By reordering, one can write

$\omega^n= x^*_1\wedge y^*_1\wedge \ldots \wedge x^*_n \wedge y^*_n.$

Authors variously define ωⁿ or (−1)^n/2ωⁿ as the standard volume form. An occasional factor of n! may also appear, depending on whether the definition of the alternating product contains a factor of n! or not. The volume form defines an orientation on the symplectic vector space (V, ω).

Symplectic map

Suppose that (V,ω) and (W,ρ) are symplectic vector spaces. Then a linear map ƒ : V → W is called a symplectic map if the pullback preserves the symplectic form, i.e. ƒ*ρ = ω, where the pullback form is defined by (ƒ*ρ)(u,v) = ρ(ƒ_∗(u),ƒ_∗(v)), where ƒ_∗ : TV → TW is the differential of ƒ. Note that symplectic maps are volume-preserving, orientation-preserving, and are vector space isomorphisms.

Symplectic group

If V = W, then a symplectic map is called a linear symplectic transformation of V. In particular, in this case one has that ω(ƒ_∗(u),ƒ_∗(v)) = ω(u,v), and so the linear transformation ƒ preserves the symplectic form. The set of all symplectic transformations forms a group and in particular a Lie group, called the symplectic group and denoted by Sp(V) or sometimes Sp(V,ω). In matrix form symplectic transformations are given by symplectic matrices.

Subspaces

Let W be a linear subspace of V. Define the symplectic complement of W to be the subspace

$W^{\perp} = \{v\in V \mid \omega(v,w) = 0 \mbox{ for all } w\in W\}.$

The symplectic complement satisfies

$(W^{\perp})^{\perp} = W$

and

$\dim W %2B \dim W^\perp = \dim V.$

However, unlike orthogonal complements, W^⊥ ∩ W need not be 0. We distinguish four cases:

W is symplectic if W^⊥ ∩ W = {0}. This is true if and only if ω restricts to a nondegenerate form on W. A symplectic subspace with the restricted form is a symplectic vector space in its own right.
W is isotropic if W ⊆ W^⊥. This is true if and only if ω restricts to 0 on W. Any one-dimensional subspace is isotropic.
W is coisotropic if W^⊥ ⊆ W. W is coisotropic if and only if ω descends to a nondegenerate form on the quotient space W/W^⊥. Equivalently W is coisotropic if and only if W^⊥ is isotropic. Any codimension-one subspace is coisotropic.
W is Lagrangian if W = W^⊥. A subspace is Lagrangian if and only if it is both isotropic and coisotropic. In a finite-dimensional vector space, a Lagrangian subspace is an isotropic one whose dimension is half that of V. Every isotropic subspace can be extended to a Lagrangian one.

Referring to the canonical vector space R²ⁿ above,

the subspace spanned by {x₁, y₁} is symplectic
the subspace spanned by {x₁, x₂} is isotropic
the subspace spanned by {x₁, x₂, ..., x_n, y₁} is coisotropic
the subspace spanned by {x₁, x₂, ..., x_n} is Lagrangian.

Heisenberg group

Main article: Heisenberg group

A Heisenberg group can be defined for any symplectic vector space, and this is the general way that Heisenberg groups arise.

A vector space can be thought of as a commutative Lie group (under addition), or equivalently as a commutative Lie algebra, meaning with trivial Lie bracket. The Heisenberg group is a central extension of such a commutative Lie group/algebra: the symplectic form defines the commutation, analogously to the canonical commutation relations (CCR), and a Darboux basis corresponds to canonical coordinates – in physics terms, to momentum operators and position operators.

Indeed, by the Stone–von Neumann theorem, every representation satisfying the CCR (every representation of the Heisenberg group) is of this form, or more properly unitarily conjugate to the standard one.

Further, the group algebra of (the dual to) a vector space is the symmetric algebra, and the group algebra of the Heisenberg group (of the dual) is the Weyl algebra: one can think of the central extension as corresponding to quantization or deformation.

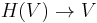Formally, the symmetric algebra of V is the group algebra of the dual, $\mathrm{Sym}(V)�:= K[V^*],$ and the Weyl algebra is the group algebra of the (dual) Heisenberg group $W(V) = K[H(V^*)].$ Since passing to group algebras is a contravariant functor, the central extension map $H(V) \to V$ becomes an inclusion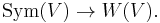 $\mathrm{Sym}(V) \to W(V).$

References

Ralph Abraham and Jarrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See chapter 3.